Let’s say I have the formula Y(n+1)= λ*Y(n)(1-Y(n))
So the value of Y at time n+1 is some factor (λ) times Y at time n times 1 minus Y at time n. Y is between 0 and 1. λ can be anything. As a starting point I choose Y0 to be 0.5 and λ=1. (In the end it actually doesn’t matter what the starting point is :-)).
Let’s iterate for a while:
(y(0)=0.5 λ=0.1 Y rounded up to 4 decimal places)
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 0.5 | 0.25 | 0.0024 | 0.0002 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
As you can see, after allready the 4th iteration the values are 0.
We can do that for a lot of λ values
| λ | 0.1 | 0.25 | 0.5 | 0.9 | 1.1 | 1.2 | 1.7 | 2.7 | 2.8 | 3,1 | 3,3 |
| Steady State | 0 | 0 | 0 | 0 | 0.0909 | 0,1667 | 0,4118 | 0,6296 | 0,6429 | 0,7646 0,5580 |
0,8236 0,4794 |
| Iteration | 4 | 7 | 12 | 70 | 71 | 31 | 6 | 22 | 41 | 24 | 14 |
Huh……with λ = 3, 1 The steady states starts to alternate after 24 iterations at 0,7646 and 0,5580. For λ = 3,3 the same thing : afte a few iterations it starts to alternate between 0,8236 and 0,4794.
Okay…..I like to see that plotted. On the X-axis λ on the y axis the steady state values:
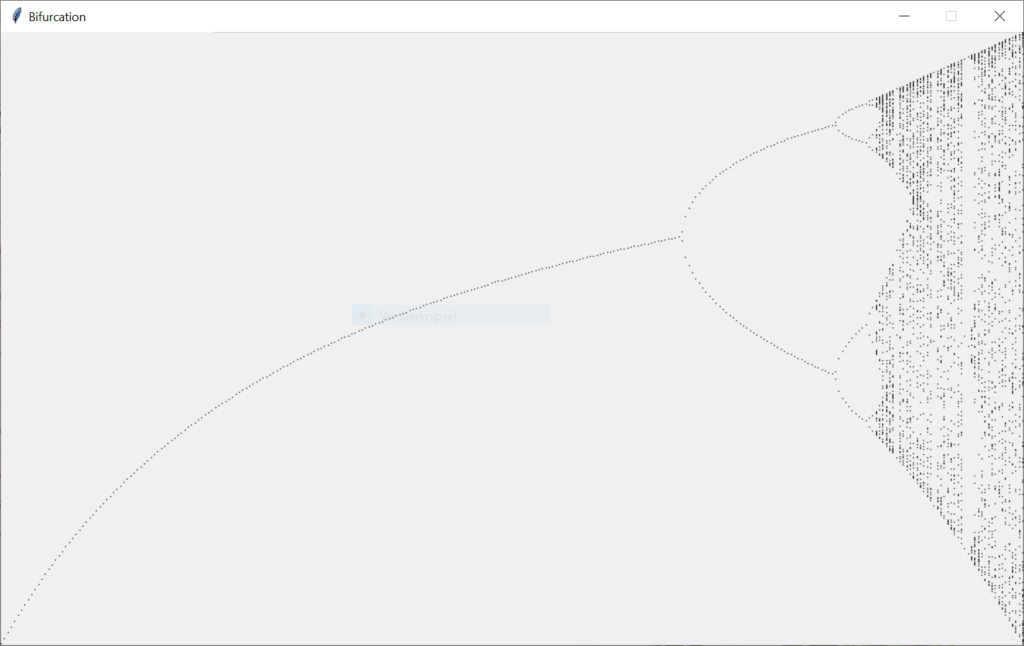
This picture starts with λ=1 on the x-axis. The stops at λ=4. You can clearly see that the graph at a certain point forks. And somehwat later the fork forks. And very soon ther is just chaos.
Let’s zoom in a little towards the right side. The X-axis starts at λ=2.8 the increment is 0.005. Some more detail is allready visible.

And zoom in even more. The X-axis starts at λ=3.5 and ends on λ=4. Iccrements are 0.001
e
To me this image is mesmerizing and unbelievable at the same time. Why does this function starts very simple, and really fast changes to chaos. After about 4…5 forks chaos comes into the picture. But…why is there a complete white area. Among all the chaos ther is an area that has almost no points.
To me this is just something to wonder about.
If you have nothing to do, and you have python on your system, you can try this yourself : bifurcation.py And if you are really bored …just take a look at the repository: github